Solve

USACO 3.1.4 Rect1

题目解答

刚一读题，第一反应就是朴素染色，但是因为较大的数据，染色法绝对行不通。因为我们没有必要重复覆盖某个点，包括计算面积我们不需要统计，而是直接用坐标计算。所以可以考虑使用面向矩形整体的方法：

  1. 二维线段树或者离散化 + 线段树：这种方法的弊端是要么过于复杂，要么MLE，所以牛刀还是用来屠牛吧
  2. 我具体论述一下矩形切割：首先通过分析我们知道凡是在后面覆盖过的绝对不会被前面的覆盖，因此假设我们覆盖第N个矩形，那么第(N-1)个一定在它的下面，由此知道要倒序染色(1)，这样可以省去很多的操作；而两个矩形相交如何处理呢？我们知道：如果两个矩形相交，他们的交集必定是一个矩形，记录一个矩形只需两个对角坐标，处理方便，所以我们要对每次的覆盖进行切割(2)；

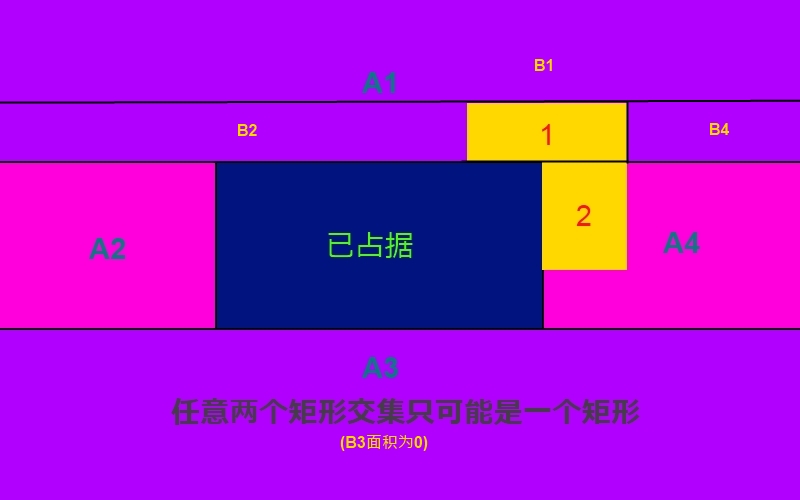
USACO 3.1.4

如图：中心深蓝色的表示当前已经覆盖的矩形，他的相邻四个A1，A2，A3，A4则是去掉已占据部分后被分割的四个矩形，也就是说凡是去掉交集都可把剩余的(未染色)部分切割成4个新矩形，包括面积为0的矩形。图中黄色的为待占据矩形，因为是倒序染色，所以忽略与已占据部分的交集，也就是说我们只需考虑未染色的部分(3)，记录未染色部分，并与未染色部分进行覆盖判断，因此黄色的与A1部分交集是 1，覆盖后，A部分又可以划分为4个新的矩形B1，B2，B3，B4(B3的面积为0)，可以看出整体是一个分治策略(4)。

综合以上(1)(2)(3)(4)条，我们对未染色部分进行处理，根据这种思路，可以不用递归，加一个链表记录所有的新的矩形，牺牲空间换取时间，平均时间复杂度O(n^2)。可以秒出。

运行结果

Compiling…
Compile: OK
Executing…
Test 1: TEST OK [0.000 secs, 2956 KB]
Test 2: TEST OK [0.000 secs, 2956 KB]
Test 3: TEST OK [0.011 secs, 2956 KB]
Test 4: TEST OK [0.000 secs, 2956 KB]
Test 5: TEST OK [0.011 secs, 2956 KB]
Test 6: TEST OK [0.000 secs, 2956 KB]
Test 7: TEST OK [0.011 secs, 2956 KB]
Test 8: TEST OK [0.011 secs, 2956 KB]
Test 9: TEST OK [0.000 secs, 2956 KB]
Test 10: TEST OK [0.011 secs, 2956 KB]
Test 11: TEST OK [0.011 secs, 2956 KB]
All tests OK.
Your program (‘rect1’) produced all correct answers! This is your
submission #2 for this problem. Congratulations! //坐标确实是本题令我头疼的地方 .

程序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
#include<fstream>
using namespace std;
ofstream fout ("rect1.out",ios::out);
ifstream fin ("rect1.in",ios::in);
const long MAX = 1001;
struct node{
  long llx,lly,urx,ury,colour;
}rect[MAX];
struct link1{
  long llx,lly,urx,ury;
  link1 *next,*up;
}*head,*tail;
long a,b,n,ans[2501];
bool quit;
inline long TMAX(long a,long b) {return (a>b?a:b);}
inline long TMIN(long a,long b) {return (a<b?a:b);}
inline bool add(long llx,long lly,long urx,long ury,link1 *t)
{
  if(llx==urx || lly==ury) return false;//the area cannot be zero
  link1 *temp=new link1;
  temp->llx=llx;
  temp->lly=lly;
  temp->urx=urx;
  temp->ury=ury;
  t->next=temp;
  temp->up=t;
  return true;
}
inline void work(int n)
{
  link1 *temp,*ttail;
  long s=0;
  for(int i=n;i>=1;i--) //倒序染色
  {
    temp=head;
    ttail=tail;
	quit=false;
    while(temp!=NULL)
    {
      if(rect[i].urx<=temp->llx || temp->urx<=rect[i].llx || rect[i].ury<=temp->lly || temp->ury<=rect[i].lly)
      {//判断是否有交集
		if(temp==tail) quit=true;//quit
		temp=temp->next;
      }
      else//扩展
      {//计算交集面积
	      long x1=TMIN(rect[i].urx,temp->urx),x2=TMAX(rect[i].llx,temp->llx),
		   y1=TMIN(rect[i].ury,temp->ury),y2=TMAX(rect[i].lly,temp->lly);
	      if(rect[i].colour!=1)
	      {
		      s=(x1-x2)*(y1-y2);
		      ans[rect[i].colour]+=s;
		      ans[1]-=s;
	      }
	      if(rect[i].ury<temp->ury) if(add(temp->llx,rect[i].ury,temp->urx,temp->ury,ttail)) ttail=ttail->next; //1
	      if(rect[i].lly>temp->lly) if(add(temp->llx,temp->lly,temp->urx,rect[i].lly,ttail)) ttail=ttail->next;//3
	      if(rect[i].llx>temp->llx) if(add(temp->llx,y2,rect[i].llx,y1,ttail)) ttail=ttail->next; //2
	      if(rect[i].urx<temp->urx) if(add(rect[i].urx,y2,temp->urx,y1,ttail)) ttail=ttail->next; //4
	      link1 *tdelete=temp;//删除扩展完毕的矩形
	      if(temp==tail) quit=true;
	      if(temp==head) { head=temp->next;head->up=NULL;}
	      else
	      {
		      temp->up->next=temp->next;
		      temp->next->up=temp->up;
	      }
	      temp=temp->next;
	      delete tdelete;
      }
      if(quit) break;
    }
    tail=ttail;//refresh
  }
}
int main()
{
  fin>>a>>b>>n;
  ans[1]=a*b;
  head=new link1;
  head->llx=0;
  head->lly=0;
  head->urx=a;
  head->ury=b;
  tail=head;
  for(int i=1;i<=n;i++)
    fin>>rect[i].llx>>rect[i].lly>>rect[i].urx>>rect[i].ury>>rect[i].colour;
  work(n);
  for(int i=1;i<=2500;i++)
    if(ans[i]!=0) fout<<i<<' '<<ans[i]<<endl;
  return 0;
}

后记

本文是百度空间的移植，附：全部USACO题目解答。