1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
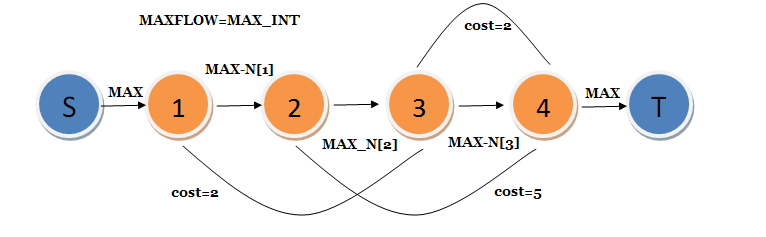
| #include<iostream>
#include<cstring>
#define BIG 40005
#define MAX 10000000
using namespace std;
struct edge{
long x,y,cap,cost;
edge *next,*target;
edge(){}
edge(int x,int y,int c,int co,edge *n):x(x),y(y),cap(c),cost(co),next(n),target(0){}
void *operator new(size_t,void *ptr){return ptr;}
}*EDGE[BIG];
long source=BIG-2,sink=BIG-1,queue[BIG],lev[BIG],dist[BIG],MAXTOT,n,m,num;
edge *Stack[BIG],*Path[BIG];
bool qin[BIG];
inline bool FindMincost(){
int tail=1,head=0,now=0;
memset(qin,0,sizeof(qin));
memset(lev,-1,sizeof(lev));
for(int i=1;i<=n+1;i++) dist[i]=MAX;
dist[sink]=MAX;
lev[source]=0;
dist[source]=0;
queue[tail]=source;
qin[source]=1;
while(head<tail){
now=queue[++head];
qin[now]=0;
for(edge *e=EDGE[now];e;e=e->next)
if(e->cap!=0 && dist[now]+e->cost<dist[e->y]){
dist[e->y]=dist[now]+e->cost;
lev[e->y]=lev[now]+1;
if(!qin[e->y]) {queue[++tail]=e->y;qin[e->y]=1;}
}
}
return (dist[sink]!=MAX);
}
inline void FindMaxFlow(){
long Lpath=1,record,delta,top=source;
memcpy(Stack,EDGE,sizeof(EDGE));
while(top>0){
if(sink==top){
delta=MAX;
for(int i=1;i<Lpath;i++)
if(delta>Path[i]->cap){
delta=Path[i]->cap;
record=i;
}
for(int i=1;i<Lpath;i++){
Path[i]->cap-=delta;
Path[i]->target->cap+=delta;
MAXTOT+=Path[i]->cost*delta;
}
Lpath=record;
top=Path[Lpath]->x;
}
edge *temE;
for(temE=Stack[top];temE;temE=temE->next)
if(temE->cap!=0 && lev[top]+1==lev[temE->y] && dist[top]+temE->cost==dist[temE->y]) break;
Stack[top]=temE;
if(temE){
Path[Lpath++]=temE;
top=temE->y;
}else{
lev[top]=-1;
dist[top]=MAX;
if(Lpath==1) return ;
top=Path[--Lpath]->x;
}
}
}
inline void BuildEdge(int x,int y,int cap,int cost){
edge *tempEDGE=new edge[3];
EDGE[x]=new((void *)tempEDGE++) edge(x,y,cap,cost,EDGE[x]);
EDGE[y]=new((void *)tempEDGE++) edge(y,x,0,-cost,EDGE[y]);
EDGE[x]->target=EDGE[y];
EDGE[y]->target=EDGE[x];
}
int main(){
cin>>n>>m;
BuildEdge(source,1,MAX,0);
BuildEdge(n+1,sink,MAX,0);
for(int i=1;i<=n;i++){
cin>>num;
BuildEdge(i,i+1,MAX-num,0);
}
long x,y;
for(int i=1;i<=m;i++){
cin>>x>>y>>num;
BuildEdge(x,y+1,MAX,num);
}
while(FindMincost())FindMaxFlow();
cout<< MAXTOT << endl;
return 0;
}
|