Solve

Hanoi Tower

题目描述

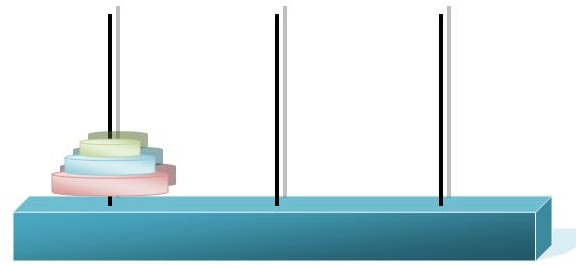
在19世纪有一种hanoi游戏，游戏的装置是一块铜板，上面有三根金刚石的针，针上放着从小到达64个盘子。游戏的目标是从一根针上移到另一根针上，还有一个针作为中间过渡。游戏规定每次只能够动一个盘子，而且大盘子永远在小盘子下面。问题： 由于移动的次数太多，标志着世界末日的到来，所以计算机不要求你计算如此多的移动方式，只要你可以算出7以内即可,
输入n =3 输出：A->C A->B C->B A->C B->A B->C A->C

题解

我们考虑一般的情况：如果想将n个盘子从a移动到c,可以划分阶段，先将n-1个盘子从a通过c移动到b,然后将a中剩下的一个盘子移动到c,最后再将n-1个盘子从b通过a移动到c。这样本来是n个盘子的问题，变成了与n-1个盘子有关的问题。所以本题可以使用递归，重复这个过程，每次n减1，直到n=1时，直接移动盘子就可以了。

Hanoi Tower

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <iostream> //这道题目很基础，只是大学学C语言，于是我就把它翻出来了。
using namespace std;

void move(int n,char a,char b,char c);

int main() {
    int n;
    cin>>n;
    move(n,'A','B','C');
    return 0;
}

void move(int n,char a,char b,char c) {
    if (n==1) cout<<a<<"->"<<c<<endl;
    else {
        move(n-1,a,c,b);
        cout<<a<<"->"<<c<<endl;
        move(n-1,b,a,c);
    }
}