题目解答 问题的本质是求所有的可能的哈密顿路径的情况,可以使用DFS+剪枝求解。
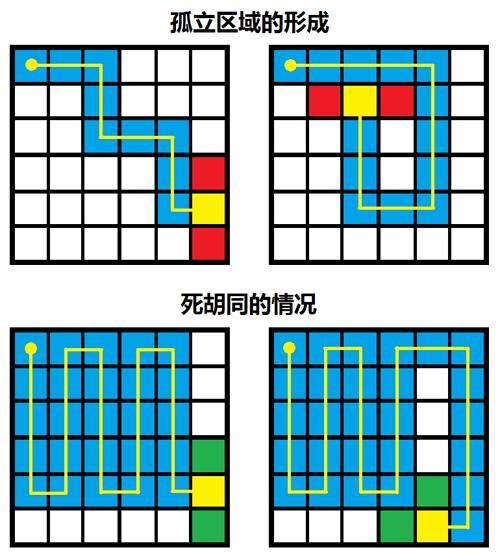
孤立区域的形成:
进入死胡同:
运行情况 Compiling…
Executing…
All tests OK.
YOUR PROGRAM (‘betsy’) WORKED FIRST TIME! That’s fantastic
程序清单 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 #include <iostream> #include <cstring> #include <string> #include <cstdio> using namespace std; bool map[9 ][9 ];int pos[][2 ] = {{0 , 1 }, {0 , -1 }, {1 , 0 }, {-1 , 0 }}, n, total; inline int getlive (int x, int y) int t = 0 ; for (int k = 0 ; k < 4 ; k++) if (!map[x + pos[k][0 ]][y + pos[k][1 ]]) t++; return t; } void dfs (int x, int y, int sum) if (x == n && y == 1 ){ if (sum == n * n) total++; return ; } if ((map[x][y-1 ] && map[x][y+1 ] && !map[x-1 ][y] && !map[x+1 ][y]) || (!map[x][y-1 ] && !map[x][y+1 ] && map[x-1 ][y] && map[x+1 ][y])) return ; int mx, my, count = 0 ; for (int i = 0 ; i < 4 ; i++){ int X = x + pos[i][0 ], Y = y + pos[i][1 ]; if (map[X][Y] || (X == n && Y == 1 )) continue ; if (getlive (X, Y) < 2 ) count++, mx = X, my = Y; } if (count > 1 ) return ; else { if (count == 1 ){ map[mx][my] = 1 ; dfs (mx, my, sum + 1 ); map[mx][my] = 0 ; } else for (int i = 0 ; i < 4 ; i++){ int X = x + pos[i][0 ], Y = y + pos[i][1 ]; if (!map[X][Y]){ map[X][Y] = 1 ; dfs (X, Y, sum + 1 ); map[X][Y] = 0 ; } } } } int main () cin >> n; for (int i = 1 ; i <= n; i++) map[1 ][1 ] = map[0 ][i] = map[n + 1 ][i] = map[i][0 ] = map[i][n + 1 ] = 1 ; dfs (1 , 1 , 1 ); cout << total << endl; return 0 ; }
注意事项 剪枝的消耗也要考虑在内。
难易等级 Medium Up(NOIP the 4th)
其他方法 基于SCC的状态压缩动态规划,参考陈丹琦集训队论文。
后记 本文是原Wordpress博客的移植,附:全部USACO题目解答 。