USACO 5.5.1 Picture

题目解答

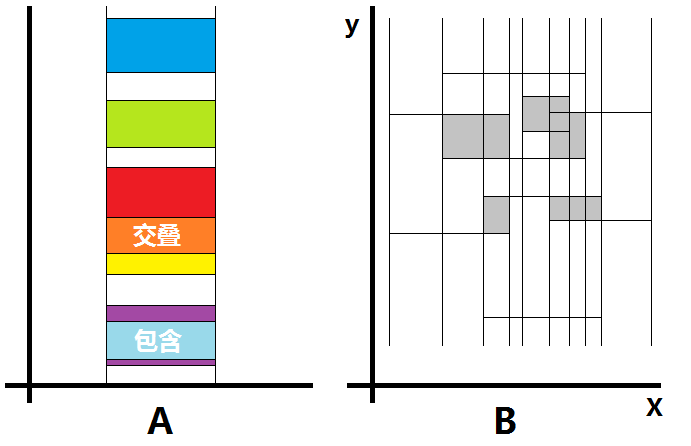
其实边界需要统计的是上下左右4个方向没有被覆盖到的边长的总和。这个问题的难点是怎样使得需要判断检索重叠的复杂度尽量小，我们先简化问题，假设所有矩形都是A情况的，也就是宽度都一样并且垂直排列，这样的话我们就将矩形的情况分为不相交，交叠，包含几种情况。先从横向的边开始看，如图所示，如果只考虑蓝色和浅绿色这两个矩形因为没有任何与其相交的其他矩形，直接统计横向边长，然而交叠和包含要怎么办呢。如图红色和黄色的矩形有橙色的部分，那么也就是说我们只用统计红色的上边长和黄色的下边长了。而浅蓝色和紫色的关系也是类似只用统计紫色的两个边。

从这里我们得到一些启发，假设所有边长都是1个单位长度，显然我们只是统计一个覆盖域的上下两个边界，那么这从抽象意义上很类似括号匹配的问题，下面的这些矩形块可以抽象成()()(())(())注意观察它们的特点，可以发现跟真实的配对没有关系，也就是()()(())(())，我们用一个栈依次压入括号，每次出现()的配对就出栈。然后要统计这些，当压入后(且栈只有这一个元素)时计数器加一，当弹出元素后栈空时计数器加一。这样我们就相当于统计出了所有的该纳入计算的边界，由这个思考点出发，我们要对所有的矩形边进行离散化，同时要区别上下边界，抽象成“左右括号”。这个时候有个细节，对于横向边我们按纵标排序，如果纵标一样谁在前？其实这也是交叠的一种情况，如果纵标一样，先要把左括号排在前，也就是如果我们按纵标由小到大排，下边界应在前，不然会使得周长变大。

具体实现时我们看B图，因为配对不只是一种情况，而且坐标很大，这时候我们可以使用线段树来辅助数据结构的部分，需要横着纵着处理两次。也就是对于类似括号匹配中栈的操作，真正实现用的是线段树。

这样本问题就解决了，算法是离散化+线段树。这个算法的正确性是我们已经排好了序，而且每个方向的边都是成对出现的。

运行情况

Compiling…
Compile: OK

Executing…
Test 1: TEST OK [0.011 secs, 5100 KB]
Test 2: TEST OK [0.011 secs, 5100 KB]
Test 3: TEST OK [0.011 secs, 5100 KB]
Test 4: TEST OK [0.011 secs, 5100 KB]
Test 5: TEST OK [0.011 secs, 5100 KB]
Test 6: TEST OK [0.011 secs, 5100 KB]
Test 7: TEST OK [0.043 secs, 5100 KB]
Test 8: TEST OK [0.011 secs, 5100 KB]
Test 9: TEST OK [0.043 secs, 5100 KB]
Test 10: TEST OK [0.011 secs, 5100 KB]
Test 11: TEST OK [0.259 secs, 5100 KB]

All tests OK.

YOUR PROGRAM (‘picture’) WORKED FIRST TIME! That’s fantastic
– and a rare thing. Please accept these special automated
congratulations.

程序清单

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#define MAX(a, b) (a > b ? a : b)
#define recv recvh
#define rech recvh
 
using namespace std;
 
struct Node{
        long lch, rch, l, r, clr, mid, all, tot;  //clr表示当前颜色,all表示整体的颜色
        bool mark;    //mark是True时杂色，False则纯色。
}tree[40005];
struct rectVH{
        int s, t, vh, start;
        bool operator < (const rectVH &cmp)const {
                if(vh == cmp.vh) return cmp.start < start;
                return vh < cmp.vh;
        }       
}recvh[20005];
long tot = 1, n, ans;
 
class regtree{
        public:
                void build(long left, long right, long index){
                        tree[index].l = left;
                        tree[index].r = right;
                        tree[index].mid = (left + right) / 2;
                        tree[index].all = right - left + 1;
                        tree[index].mark = tree[index].clr = tree[index].tot = 0;
                        if(left < right){
                                tree[index].lch = ++tot;
                                build(left, tree[index].mid, tot);
                                tree[index].rch = ++tot;
                                build(tree[index].mid + 1, right, tot);
                        }
                }
 
                void insert(long left, long right, long index, int delta){
                        if(tree[index].l >= left && tree[index].r <= right) 
                                if(!tree[index].mark){ //lazy
                                        tree[index].clr += delta;
                                        if(tree[index].clr == 1 && delta > 0)
                                                ans += tree[index].all;
                                        if(tree[index].clr == 0 && delta < 0)
                                                ans += tree[index].all;
                                        return;
                                }
                        if(!tree[index].mark && tree[index].all != 1){ //下放
                                tree[tree[index].lch].clr = tree[index].clr;
                                tree[tree[index].lch].mark = false;
                                tree[tree[index].rch].clr = tree[index].clr;
                                tree[tree[index].rch].mark = false;
                        }
                        if(tree[index].all == 1) return; //不递归叶子结点
                        if(left <= tree[index].mid && tree[index].lch != 0)
                                insert(left, right, tree[index].lch, delta); 
                        if(right > tree[index].mid && tree[index].rch != 0)
                                insert(left, right, tree[index].rch, delta);
                        tree[index].mark = true;    //先归为杂色，因为递归后有可能是杂色
                        if(!tree[tree[index].lch].mark && !tree[tree[index].rch].mark && 
                                (tree[tree[index].lch].clr == tree[tree[index].rch].clr)) //恢复统一色，如果可能
                                tree[index].mark = false, 
                                tree[index].clr = tree[tree[index].lch].clr;
                }
}line;
 
int main(){
        tree[0].mark = false;       //边界条件     
        cin >> n;
        int N2 = n * 2, N3 = n * 3;
        for(int i = 1; i <= n; i++){
                int lx, ly, rx, ry;
                scanf("%d%d%d%d", &lx, &ly, &rx, &ry);
                lx += 10000, ly += 10000, rx += 10000, ry += 10000;
                recv[i].s = ly, recv[i].t = ry - 1;
                recv[i].vh = lx, recv[i].start = true;
                recv[i + n].s = ly, recv[i + n].t = ry - 1;
                recv[i + n].vh = rx, recv[i + n].start = false;
                rech[i + N2].s = lx, rech[i + N2].t = rx - 1;
                rech[i + N2].vh = ly, rech[i + N2].start = true;
                rech[i + N3].s = lx, rech[i + N3].t = rx - 1;
                rech[i + N3].vh = ry, rech[i + N3].start = false;
        }
        sort(recvh + 1, recvh + N2 + 1);
        sort(recvh + N2 + 1, recvh + n + N3 + 1);
        tot = 1, line.build(0, 20000, 1);   //纵向的边
        for(int i = 1; i <= N2; i++)
                line.insert(recvh[i].s, recvh[i].t, 1, (recvh[i].start ? 1 : -1));
        memset(tree, 0, sizeof(tree));
        tot = 1, line.build(0, 20000, 1);   //横向的边
        for(int i = N2 + 1; i <= N3 + n; i++)
                line.insert(recvh[i].s, recvh[i].t, 1, (recvh[i].start ? 1 : -1));
        cout << ans << endl;
        return 0;
}

注意事项

如果排序时出现一样值的情况，要处理优先级。

难易等级

Hard down(省选/NOI)

后记

本文是原Wordpress博客的移植，附：全部USACO题目解答。