Solve

USACO 6.1.2 Vans

题目解答

找规律。第一张图和第二张图其实已经暗示了这道题目的潜在规律。注意到从一个第一行的点横向出发再回到这个点只有从这个点下面的点回来。定义F[i]表示从前i列中第i列的第2个点到第1个点共有多少合法路径，根据这个定义F[n]即为所求。G[i]表示前i列中第i列的第1个点到第4个点共有多少路径。因此可以推出F[i] = F[i-1] + G[i-1] (画图找规律)。

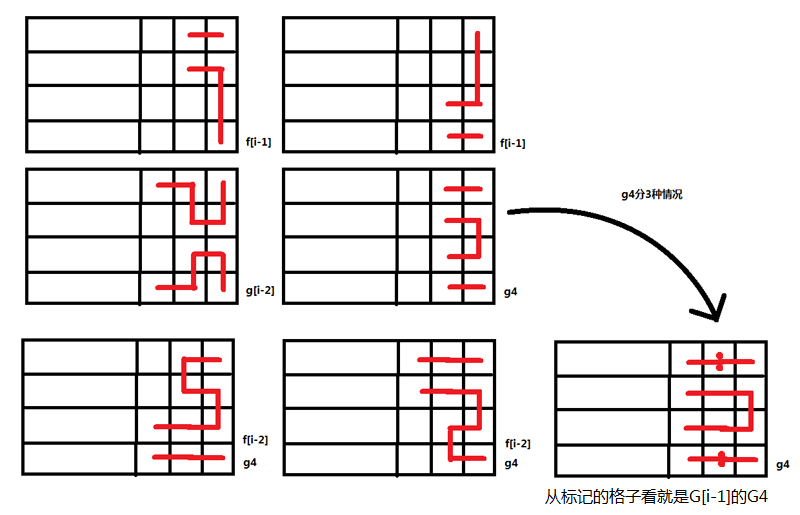
下面我们仔细观察这两个方程的定义，从而化简方程，如下图：

G[i] = F[i-1] * 2 + G[i-2] + G4[i] (1)

G4[i] = F[i-2] * 2 + G4[i-1] (2)

由(1)化简(2)式得到：G4[i] = G[i-1] - G1[i-1] - G2[i-1] - G3[i-1] + F[i-2] * 2 = G[i-1] - G[i-3]

所以G[i] = F[i-1]*2 + G[i-1] + G[i-2] - G[i-3] (3)

又由F[i] - F[i-1] = G[i-1] (4)

最终我们得到 F[n] = 2F[n-1] + 2F[n-2] - 2F[n-3] + F[n-4] (n>=5)

初始值：F[1] = 0; F[2] = 2; F[3] = 4; F[4] = 12。

USACO 6.1.2

运行结果

Compiling…
Compile: OK

Executing…
Test 1: TEST OK [0.000 secs, 3388 KB]
Test 2: TEST OK [0.000 secs, 3388 KB]
Test 3: TEST OK [0.000 secs, 3388 KB]
Test 4: TEST OK [0.000 secs, 3388 KB]
Test 5: TEST OK [0.000 secs, 3520 KB]
Test 6: TEST OK [0.000 secs, 3784 KB]
Test 7: TEST OK [0.000 secs, 4048 KB]
Test 8: TEST OK [0.000 secs, 4576 KB]
Test 9: TEST OK [0.000 secs, 6952 KB]
Test 10: TEST OK [0.011 secs, 9328 KB]
Test 11: TEST OK [0.032 secs, 15136 KB]

All tests OK.

YOUR PROGRAM (‘vans’) WORKED FIRST TIME! That’s fantastic
– and a rare thing. Please accept these special automated
congratulations.

程序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include <iostream>
#include <cstring>
#include <cstdio>

#define MAX(a, b) (a > b ? a : b)

using namespace std;

struct Node{
  Node(){
    memset(num, 0, sizeof(num));
    len = 0;
  }
  int num[500], len;
  
  friend Node operator +  (const Node &A, const Node &B){
    Node *C = new Node;
    int  LEN = MAX(A.len, B.len);
    for (int i = 1; i <= LEN; i++){
      C->num[i] += A.num[i] + B.num[i];
      C->num[i + 1] += C->num[i] / 10;
      C->num[i] %= 10;
    }
    if(C->num[LEN + 1]!= 0) C->len = ++LEN;
    else  C->len =LEN;
    return  *C;
  }

  friend Node operator -  (const Node &A, const Node &B){
    Node *C = new Node;
    *C = A;
    int  LEN = A.len, jinwei = 0;
    for (int i = 1; i <= LEN; i++){
      if(C->num[i] < B.num[i]){
        C->num[i] += 10;
        for(int j = i + 1; j <= LEN; j++){
          C->num[j]--;
          if(C->num[j] >= 0) break;
          else C->num[j] += 10;
        }
      }
      C->num[i] -= B.num[i];
    }
    if(!C->num[LEN]) C->len;
    return  *C;
  }

  void operator =  (const Node &A){
    for(int i=1; i <= A.len; i++)  num[i] = A.num [i];
    len = A.len ;
  }

  void print(){
    for(int i = len; i >= 1; i--) 
      printf("%d", num[i]);
    printf("\n");
  }
}dp[6];
int n;

int main(){
	freopen("vans.in", "r", stdin);
	freopen("vans.out", "w", stdout);
	cin >> n;
	dp[1].len = 1;
	dp[2].len = 1, dp[2].num[1] = 2;
	dp[3].len = 1, dp[3].num[1] = 4;
	dp[4].len = 2, dp[4].num[1] = 2, dp[4].num[2] = 1;
	if(n >= 5)
		for(int i = 5; i <= n; i++){
			dp[5] = dp[4] + dp[4] + dp[3] + dp[3] + dp[1] - dp[2] - dp[2];
			dp[1] = dp[2], dp[2] = dp[3], dp[3] = dp[4], dp[4] = dp[5];
		}
	dp[(n >= 5 ? 5 : n)].print();
	return 0;
}

后记

本文是百度空间的移植，附：全部USACO题目解答。