浅谈一下缓存中的LRU与LFU策略,针对get(key)和put(key,value)两个接口实现任何操作时间复杂度O(1)的数据结构。
LRU
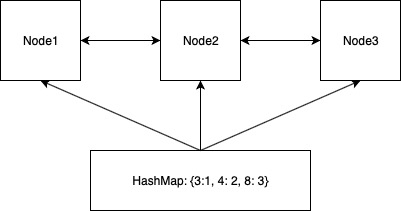
我们维护一个队列,这个队列永远把最近插入/使用的放在顶端,最小最近使用的放在底端。对于put方法要么更新已有的值,要么新加入一个值,无论更新还是新插入都要放在顶端,如果当前队列已满并且还需要插入新值,则删除底端的值后再插入新的值。对于get方法,要么没找到返回-1,要么返回查询结果,并把这个值放在顶端。
上述策略可以满足LRU,但是如何保证操作都是O(1)呢?我们比较耗时的操作是在挪动value的位置,比如更新一个value后,要将其放在队列的顶端。如果是一般的Array存储,那么时间复杂度是O(n),所以我们选择双向链表。但是这样一来查找的复杂度就变成O(n)了,我们只需要用hashmap辅助,hashmap的value记录每个链表结点的引用即可。
这样删除的时候,直接删除尾指针指向的结点,并删除hashmap中的pair。在挪动结点的时候是不必更新hashmap的,因为hashmap存储的是引用而非绝对位置。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
class Node:
def __init__(self, key: int, value: int):
self.key = key
self.value = value
self.pre = None
self.next = None
class LRUCache:
def __init__(self, capacity: int):
self.cap = capacity
self.linkedMap = {}
self.head = Node(-1, -1)
self.tail = Node(-1, -1)
self.head.next = self.tail
self.tail.pre = self.head
def get(self, key: int) -> int:
if key in self.linkedMap:
node = self.linkedMap[key]
self._remove(node)
self._add(node)
return node.value
return -1
def put(self, key: int, value: int) -> None:
if key in self.linkedMap:
self._remove(self.linkedMap[key])
elif len(self.linkedMap) + 1 > self.cap:
self._remove(self.tail.pre)
self._add(Node(key, value))
def _remove(self, node: Node):
node.pre.next = node.next
node.next.pre = node.pre
self.linkedMap.pop(node.key)
def _add(self, node: Node):
node.next = self.head.next
node.pre = self.head
self.head.next.pre = node
self.head.next = node
self.linkedMap[node.key] = node
|
LFU
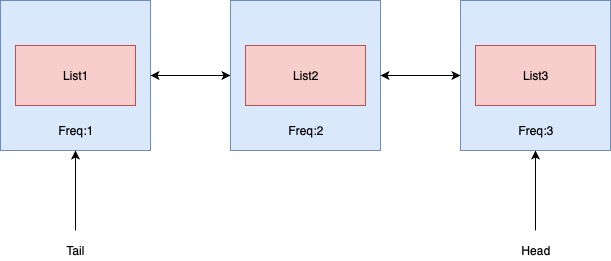
与LRU一样要用双向链表存储结点,针对每一个频率都用一个单独的链表存储,不同的频率链表之间按顺序首尾相连,逻辑上可以看作链表的链表。新加入的value都要放入频率为1的链表的表头,这是初始情况。当更新一个结点时,比如频率3的被get了一次,那么要把他从频率3的链表拿出来放入频率4的链表的表头,这样put和get的更新操作都是O(1)的复杂度。
删除的时候,我们都从频率最小的链表的末尾开始删除,也就是tail指针始终指向当前频率最小的链表的末尾,tail指针的维护时间复杂度也是O(1)的。(为了实现方便,我这部分不是严格O(1)的)
同样用hashmap保存key到node的映射,这一点和LRU是一致的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
|
class Node:
def __init__(self, k, v):
self.key = k
self.value = v
self.freq = 0
self.next = None
self.prev = None
class LFUCache:
def __init__(self, capacity: int):
self.cap = capacity
self.freqHead = {}
self.freqTail = {}
self.keyMap = {}
def get(self, key: int) -> int:
ans = -1
if key in self.keyMap:
node = self.keyMap[key]
ans = node.value
self._update(node)
return ans
def _print(self, tail):
x = []
while tail:
x.append(tail.value)
tail = tail.prev
print(x)
def put(self, key: int, value: int) -> None:
if self.cap == 0:
return
if key in self.keyMap:
self.keyMap[key].value = value
self._update(self.keyMap[key])
return
elif len(self.keyMap) == self.cap:
self._removeTail()
node = Node(key, value)
node.freq = 1
self._addFreq(node.freq, node)
def _update(self, node):
key, value, freq = node.key, node.value, node.freq
self._remove(node)
self._addFreq(freq + 1, Node(key, value))
def _removeTail(self):
tail = self.freqTail[1]
while tail and tail.key == -1:
tail = tail.prev
self._remove(tail)
def _addFreq(self, freq, node):
head = None
if freq in self.freqHead:
head = self.freqHead[freq]
else:
head = Node(-1, -1)
tail = Node(-1, -1)
head.next = tail
tail.prev = head
if freq > 1:
tail.next = self.freqHead[freq - 1]
tail.next.prev = tail
self.freqHead[freq] = head
self.freqTail[freq] = tail
self._add(node, head)
node.freq = freq
def _remove(self, node):
node.prev.next = node.next
node.next.prev = node.prev
self.keyMap.pop(node.key)
def _add(self, node, head):
node.next = head.next
node.prev = head
head.next.prev = node
head.next = node
self.keyMap[node.key] = node
|
总结
某单一类型的数据结构不足以支撑当前的需求时,可以使用多种数据结构组合完成任务。

