这道题目是一道好题，因为可以从多个角度出发考虑，途径很多。首先，乍一看题貌似是Hanoi塔的模式，只不过增加了特定的限制(不可以向回走)，先分析一个例子：石墩有2个，荷叶3个的情况。这种情况可以有至多16只青蛙过河。首先有4只先到一号石墩，接着另有4个号码较大的到达2号墩，这是很容易做到的，然后让1号墩上的3个小的跳到荷叶上，1号墩剩下那只直接跳到2号，3个荷叶上的再跳到2号。此时2号墩已经饱和了(推一下即可知道)，而1号和荷叶是空的让其饱和，则可再次有7只青蛙，此时已经有15只青蛙。左岸的第16只可以直接跳到右岸，而且可以发现怎样跳过来还可以怎样跳回去，只不过我们不跳到左岸而是右岸，这是对称的。因此可以有16只。
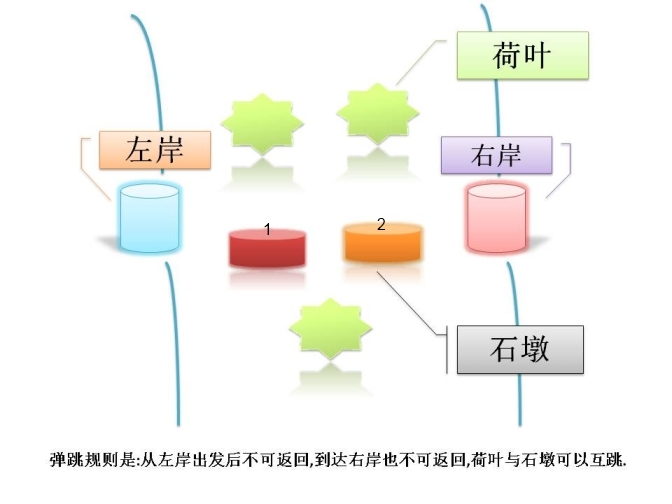
事实上，我们仔细分析可以发现，只有荷叶的话，那么最多只能有荷叶数加1只青蛙可以过河，因为过河顺序是单向传递的。所以我们如果想使过河数最大可以令青蛙在河中央停留的只数达到最多，这样只有荷叶的话必然是荷叶数加1只青蛙可以渡过。但是存在石墩就不一样了。因为石墩上可以有多只编号严格递减的青蛙。首先荷叶可以作为跳板，并由这些跳板使多只青蛙到达河中的石墩，并且尽量可以积累的多一些。而且河中的石墩是无所谓顺序的，所以我们可以这样来看待问题：
把左岸，河中央，右岸分为3个阶段。把河中的石墩当作目的地，用样例来说：根据前面的分析，1号石墩可以有4只青蛙，2号同样可以有4只，此时1、2号石墩的青蛙序号严格递减，所以1号的青蛙又可以看作右岸借助荷叶到达2号石墩。2号就有8只。此时因为2号石墩的青蛙数的总数比荷叶石墩的总数还多，所以2号石墩已经饱和。1号已空，再重复之前的工作……如此反复进行：i号石墩总可以包含(i-1)号，即以1号石墩的青蛙作为单位青蛙数s，会有s，2 * s，4 * s……只，所以总共会有2^h*(k+1)个青蛙可以过河。得到通项公式。
刚一读题，第一反应就是朴素染色，但是因为较大的数据，染色法绝对行不通。因为我们没有必要重复覆盖某个点，包括计算面积我们不需要统计，而是直接用坐标计算。所以可以考虑使用面向矩形整体的方法：
新年第一题：这道题目很值得一说，首先这是一个比较典型的计算几何转化为图论去做，同时也是需要结合两者的不错的题目。大体思想是首先用向量法计算出第4个点，因为第4个点是现有的3个点中的作为现有RT三角形的一个对角点，所以先要确定直角点，用点积为0判定，剩下的很简单了。接着要建模为一张图，然后计算最短路径。大体就是这样。
关于计算最短路径：我的想法是先求出所有点对的最短路径，然后遍历A市与B市的飞机场选出一个最短的，但是这样似乎麻烦而且时效低，所以我介绍一下官方的强大方法：首先对于A市和B市，把他们的铁路价格都改为0，这样无论选择两个城市中的哪个机场，都不用额外花费铁路价格，把城市封装为一个整体，意味着A、B的机场任意。做一遍Dijkstra即可。