Solve

USACO 3.4.1 Fence

题目解答

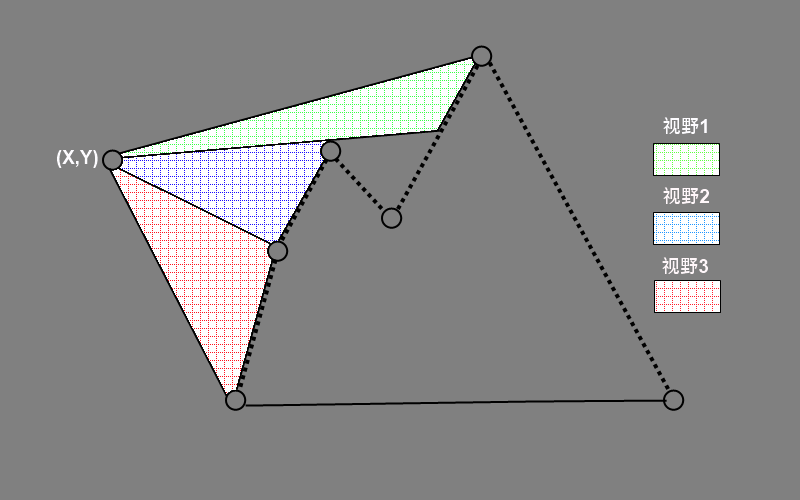
第一个计算几何问题，计算几何问题必须要“踏踏实实”的来，但是也有优化。对于本题目，我使用的是2分法。(我只想到了这个方法，听说还有强大的类似线段树的方法)。首先第一问：使用叉积判断任意两条线段是否绝对相交，若有则输出“NOFENCE”并结束。重点是第二问。观察下图。我们可以很清楚的知道，如果一条线段可以被观察到，他的视野一定不为0，因此，我们只要先找到待观察线段的中点，并与观察点连线就能得到一条新的线段(中位线)。并用新的线段与其它所有线段进行绝对相交判断。同时还要考虑非绝对相交，被点挡住的情况。如果有中位线满足不与所有点相交，那么他一定可以被看到。否则2分。边界条件是两个端点挨在一起了，说明没有满足。这时就要考虑控制精度了。一旦精度过高就会超时。反之就会漏解。(0.005就不错(^o^))具体的实现请看程序。

提一句输出：我们按顺序2分，这样在输出序列里的就是有序的，只是当最后的结点坐标一样时要按输入文件的顺序输出。而只有当第(N-1)与第N个同时要输出时才会不满足(至于为什么不多作解释)。这时先输出N，再输出(N-1)

USACO 3.4.1

运行结果

Compiling…
Compile: OK
Executing…
Test 1: TEST OK [0.011 secs, 2940 KB]
Test 2: TEST OK [0.011 secs, 2940 KB]
Test 3: TEST OK [0.000 secs, 2940 KB]
Test 4: TEST OK [0.022 secs, 2940 KB]
Test 5: TEST OK [0.000 secs, 2940 KB]
Test 6: TEST OK [0.054 secs, 2940 KB]
Test 7: TEST OK [0.216 secs, 2940 KB]
Test 8: TEST OK [0.194 secs, 2940 KB]
Test 9: TEST OK [0.194 secs, 2940 KB]
Test 10: TEST OK [0.270 secs, 2940 KB]
Test 11: TEST OK [0.000 secs, 2940 KB]
Test 12: TEST OK [0.011 secs, 2940 KB]
All tests OK.
Your program (‘fence4’) produced all correct answers! This is your
submission #3 for this problem. Congratulations!

程序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include<fstream>
#include<cmath>
using namespace std;
ofstream fout ("fence4.out",ios::out);
ifstream fin ("fence4.in",ios::in);
const double JD = 0.005;
struct Point{
    double x,y;
}point[201],see;
struct Line{
    Point start,end;
}line[201];
long n,len=0;
bool cansee[201],reg[201];
inline double crossproduct(Point start,Point U,Point V){//计算叉积
    double Ux=U.x-start.x,Uy=U.y-start.y,Vx=V.x-start.x,Vy=V.y-start.y;
    return (Ux*Vy-Uy*Vx);
}
inline int cancross(Line A,Line B){
    double A1=crossproduct(A.start,A.end,B.start),A2=crossproduct(A.start,A.end,B.end),
        B1=crossproduct(B.start,B.end,A.start),B2=crossproduct(B.start,B.end,A.end);
    if(A1==0 || A2==0) return -1;//被点挡住,A为中位线时,以A为轴,有0就表明被点挡住了.
    if(A1*A2<0 && B2*B1<0) return 1;//严格相交
    return 0;
}
inline bool check(const Line &mid){
    for(int i=1;i<=n;i++) if(!reg[i])
        if(cancross(mid,line[i])!=0) return false;
    return true;
}
inline bool watch(Point start,Point end){
    if(sqrt(((start.x-end.x)*(start.x-end.x))+((start.y-end.y)*(start.y-end.y)))<JD) return false ;
    Line mid;//中位线
    bool temp= false;
    mid.end.x=(start.x+end.x)/2;
    mid.end.y=(end.y+start.y)/2;
    mid.start.x=see.x;
    mid.start.y=see.y;
    if(check(mid)) return true ;
    else{
        temp=watch(start,mid.end);
        if(!temp) temp=watch(mid.end,end);
    }
    return temp;
}
int main()
{
    fin>>n>>see.x>>see.y;
    fin>>point[1].x>>point[1].y;
    for(int i=1;i<=200;i++) cansee[i]= false;
    for(int i=2;i<=n;i++){
        fin>>point[i].x>>point[i].y;
        line[i-1].start=point[i-1];
        line[i-1].end=point[i];
    }
    line[n].start=point[1];
    line[n].end=point[n];
    for(int i=1;i<n;i++)
        for(int j=i+1;j<=n;j++)
            if(cancross(line[i],line[j])==1){fout<<"NOFENCE"<<endl; return 0;}
    for(int i=1;i<=n;i++){
        if(crossproduct(see,line[i].start,line[i].end)==0) continue; //cut
        reg[i]= true;//不要跟自己比较
        if(watch(line[i].start,line[i].end)){len++; cansee[i]=true;}
        reg[i]= false;
    }
    fout<<len<<endl;
    if(cansee[n]&&cansee[n-1]){ //如果最后两个都合法,交换
        Line temp=line[n];
        line[n]=line[n-1];
        line[n-1]=temp;
    }
    for(int i=1;i<=n;i++) if(cansee[i])
        fout<<line[i].start.x<< ' '<<line[i].start.y<<' ' <<line[i].end.x<<' '<<line[i].end.y<<endl;
    return 0;
}

后记

本文是百度空间的移植，附：全部USACO题目解答。